SVM 支持向量机:硬间隔、软间隔、L1正则、L2正则以及核方法的讨论及代码实现
对SVM问题的一瞥
SVM他是用来解决哪类问题的?我们为什么需要SVM?
在人工智能和大数据分析的学科中,我们经常需要把数据进行进行分类,亦或是需要在数据之间找到一个最合适的分界线,来分类两类数据。举例来说,假如说我们收集了14个人的BMI值进行分析,我们希望在数据中间找到最合适的一个的值,并以此为界来判断一个人是否肥胖。假定我们收集的数据如图:

假如说我们寻找到的决定边界(decision boundary)是上图中所示橙线,那么所有在橙线右边的点我们都可以认定为”肥胖“,所有在橙线左侧的点我们都可以认定为”正常“。假如说我们收集到了一个新的数据并把它标记成为黑点,我们发现黑点在橙线右侧,由此我们推论出这个人是”肥胖“的。
当我们考虑如何去放置这个橙色的线的时候,我们发现其实他只要放在绿点和橙点的中间,在任意位置都是可以的。那么是否存在一个最适合的橙色的线呢?或者说我们该如何去寻找一个最合适的“界”呢?
这便是SVM算法真正的核心所在。
从最简单问题入手:硬间隔向量机(Hard Margain SVM)
假设,我们的数据集是两堆完全没有重合的点,并且线性可分,那么这个时候我们就可以用最简单的硬间隔向量机(Hard Margain SVM)解决此类问题。假如我们的数据如下图所示:
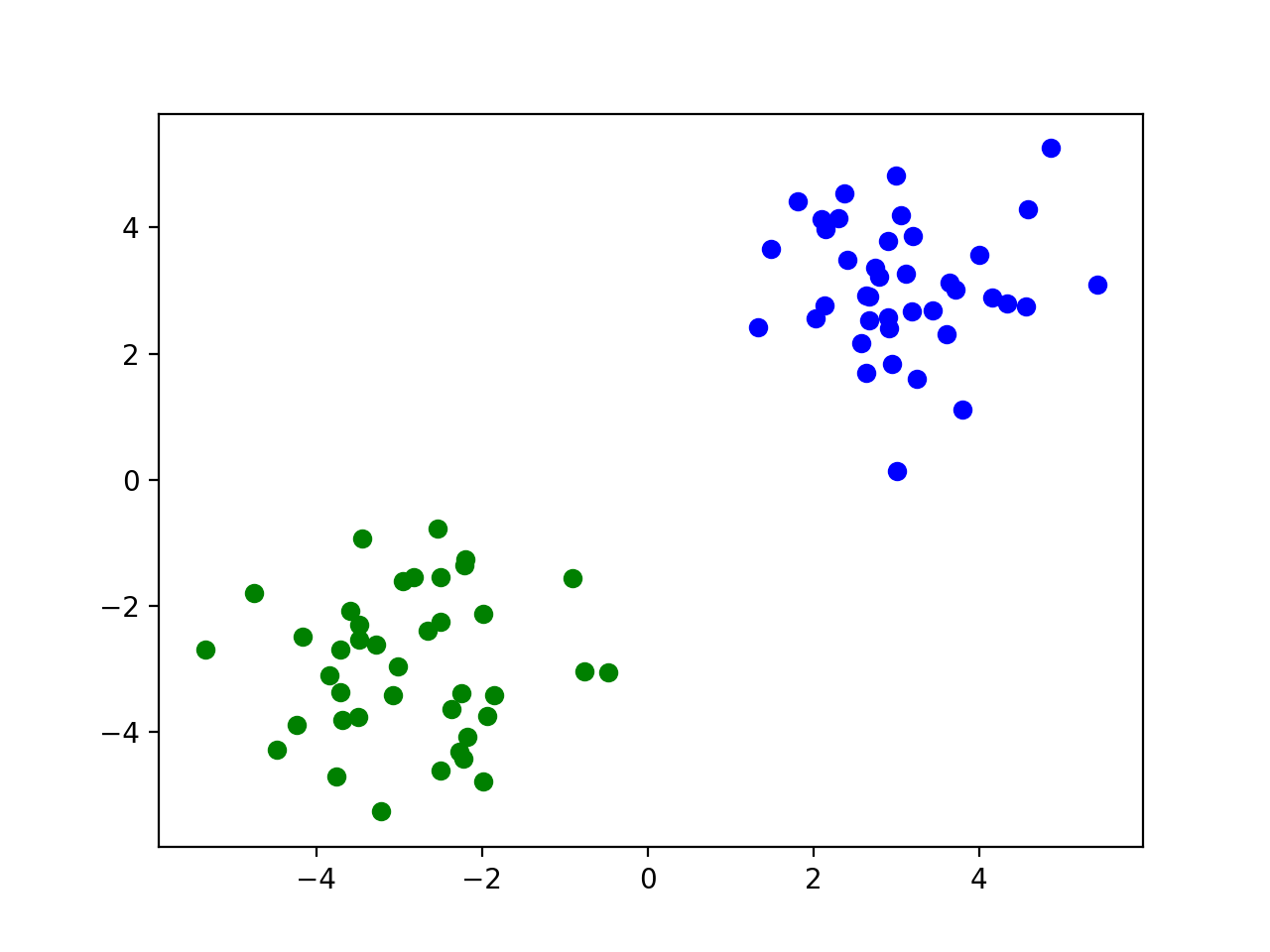
那么现在我们的问题来了,对于这种情况我们该如何分离两类点并且找到最优的解呢?
假设我们现在定义一条线 作为我们的决定边界:
我们同时定义两条平行于 的线, 使得 经过到 最近的蓝点,并且 经过到 最近的绿点。我们称为 为我们的支持向量(Support Vector)
现在我们尝试一些不同的 , 然后进行观察:
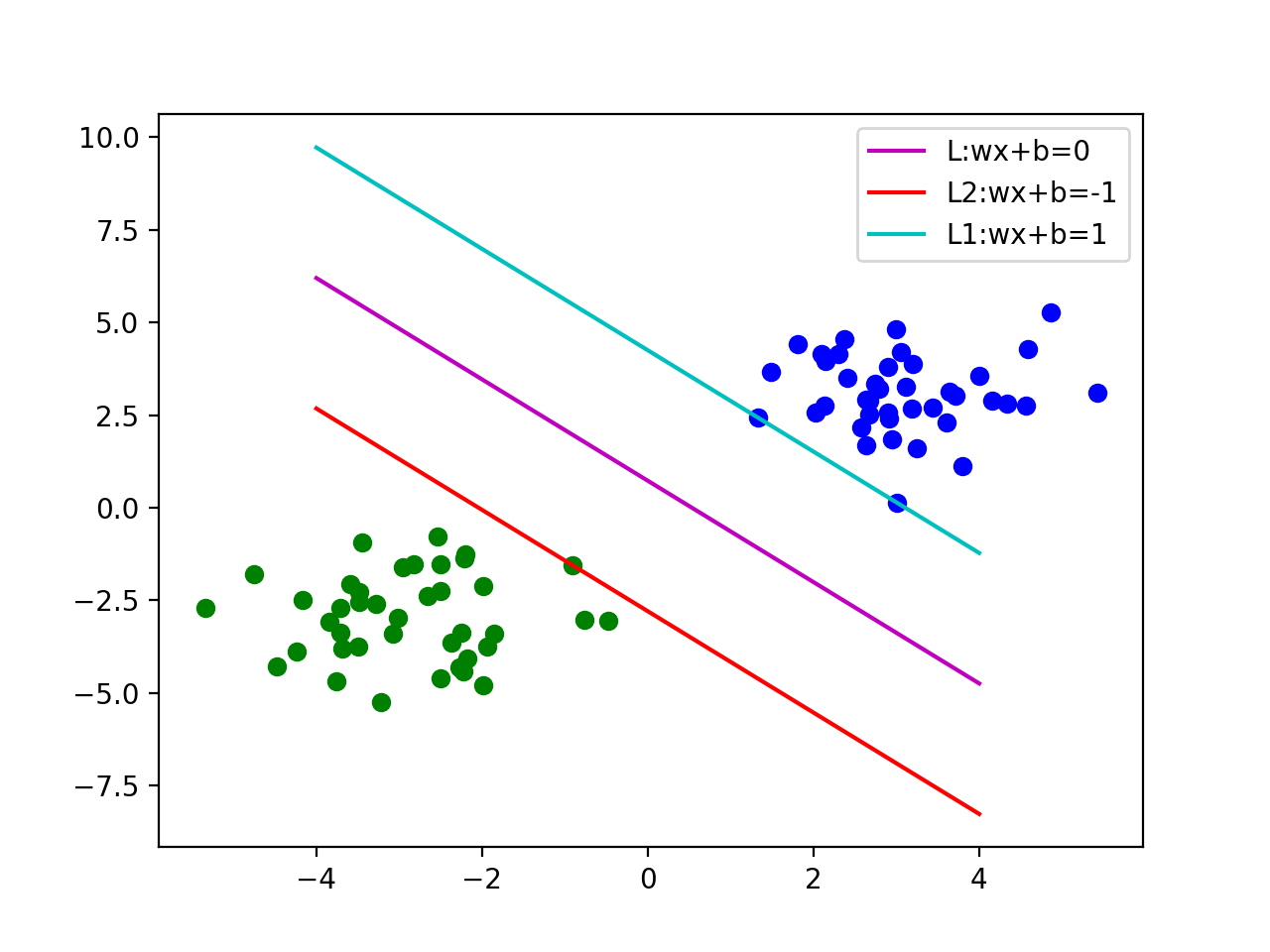
假设我们现在用第一组, 获得了第一个决定边界如上图
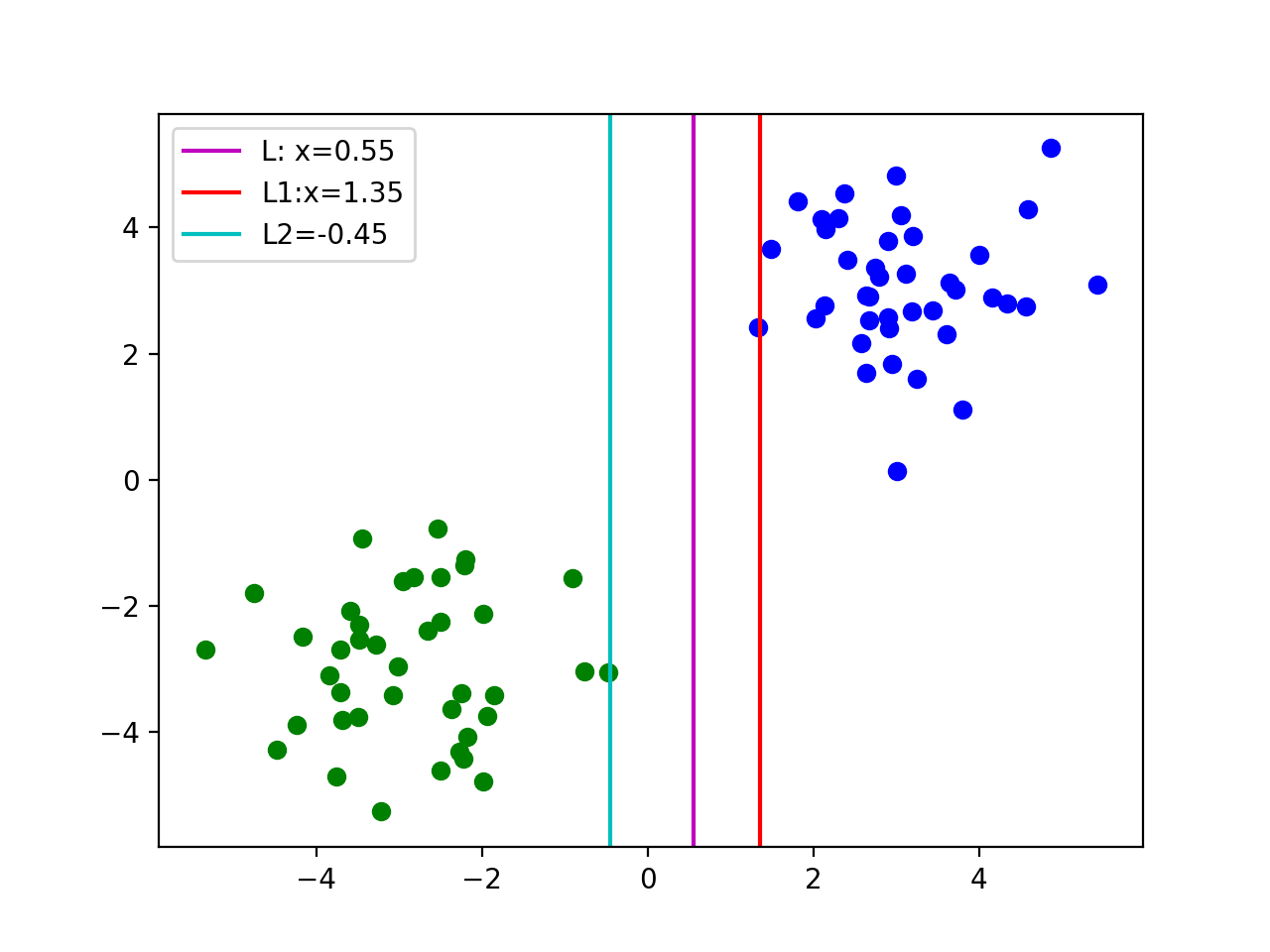
我们现在尝试变动一下我们的的值,我们获得了第二个决定边界。通过观察我们发现当之间的距离越大的时候,我们的两类点被决策边界分的越开,我们的决策边界也就越趋近于最优解
换言之,我们将寻找“界”的问题变成了一个寻找距离最大值的数学问题
我们注意到 到 与 的距离相等,也就是说我们可以转化我们的问题为“寻找最大距离的问题”,即:
同时,我们对这个最值问题也有约束(constraint), 我们需要用这个约束把所有的蓝点(), 和绿点()分开。即:
化简可得:
注: 化简的过程其实很简单,但第一次想可能还是会有些困惑,不妨带几个数就可以想明白。
到这一步,我们把这个寻找界的问题已经化简成为了一个在约束内寻找最值的纯数学问题,而这类问题可以被Python CVXPY包内的函数所解,也就是我们现在可以上手尝试代码实现我们的SVM了。
硬间隔SVM的代码实现
数据定义
在我们开始正式进行我们的代码实现前,我们需要先明确我们的数据输入。我们数据为X和y,其中X是一个numpy.ndarray, X中包含了所有点的坐标;y是一个list,其中用1和-1来区分对应X中每个点类的分类,1位蓝点,-1位绿点。
我们现在开始为我们的硬间隔SVM生成一个玩具集:
ximport numpy as npnp.random.seed(5)# 我们先生成以(3,3) 和 (-3,-3)为中心各生成40个坐标x1 = np.random.normal(3, 1, (2, 40))x2 = np.random.normal(-3, 1, (2, 40))plt.scatter(x1[0, :], x1[1, :], color='blue')plt.scatter(x2[0, :], x2[1, :], color='green')def join_data(dat1, dat2): lst = [] for i in range(len(dat1[0])): lst.append([dat1[0][i], dat1[1][i]]) for j in range(len(dat2[0])): lst.append([dat2[0][j], dat2[1][j]]) return np.asarray(lst)# 然后我们把生成好的坐标化为我们所需的标准输入格式X = join_data(x1, x2)y = [1] * len(x1[0]) + [-1] * len(x2[0])
编写硬间隔SVM
经过我们上面的讨论,我们最后把硬间隔SVM化成了以下问题:
在使用CVXPY包的情况下,这个问题可以被转化成:
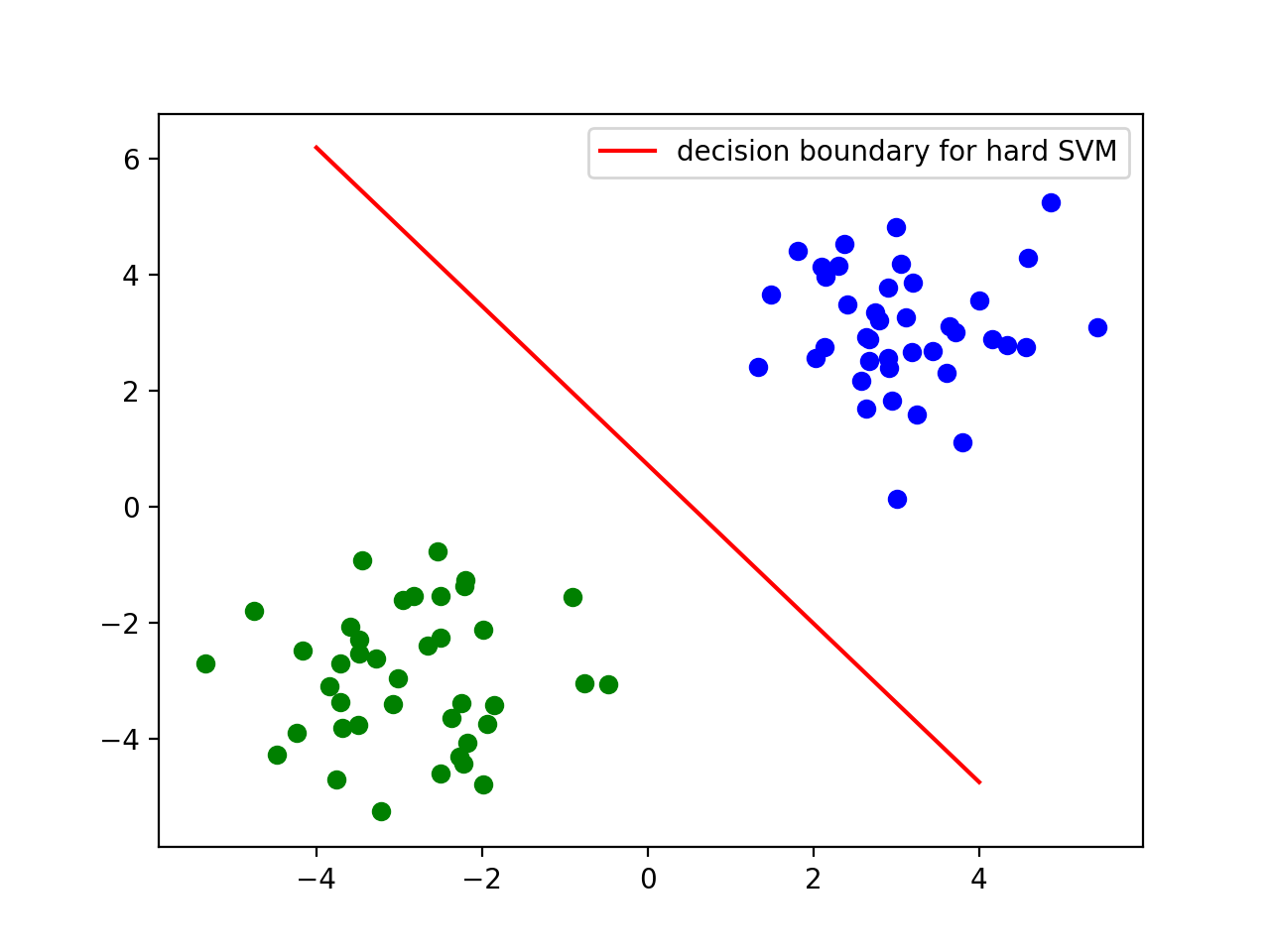
xxxxxxxxxximport cvxpy as cpimport matplotlib.pylab as pltD = X.shape[1]N = X.shape[0]W = cp.Variable(D)b = cp.Variable()# 计算损失函数loss还有约束constraint。loss = cp.sum_squares(W)constraint = [y[i]*(X[i]*W+b) >= 1 for i in range(len(y))]prob = cp.Problem(cp.Minimize(loss), constraint)prob.solve()# 转换w和b的值w = W.valueb = b.value# 画出决定边界x = np.linspace(-4, 4, 20)plt.plot(x, (-b - (w[0] * x)) / w[1], 'r', label="decision boundary for hard SVM")plt.legend()plt.show()经过以上代码,你应该可以得到一个如下图的决定边界。
硬间隔SVM的局限:假如数据有异常值,或者两组点有重合或者略微的相交?
在硬间隔SVM中,我们的决策边界把所有的点都完全正确的分开,虽然这个方法能很“准确”的分开所有的点,但是该方法对异常值会非常敏感。举例来说,假如我们在我们的玩具数据中加入一个异常值,并再用硬间隔SVM对两类点进行区分,那么我们得到的决策边界(如下图)将有悖于常识的认知。
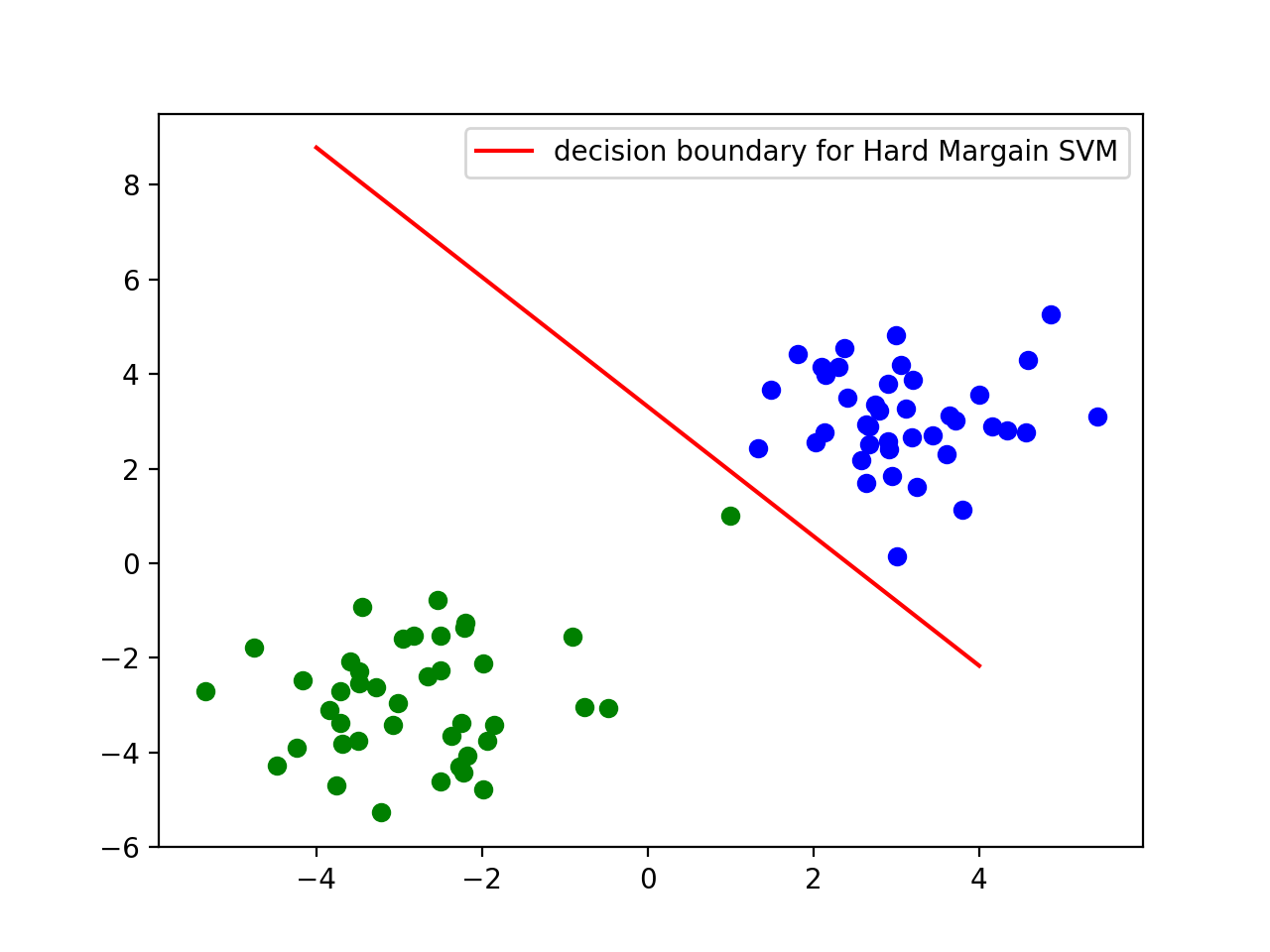
对硬间隔支持向量机缺陷的弥补:软间隔支持向量机或L1正则支持向量机(Soft Margin SVM or L1 regularzation SVM)
我们在之前的图像中很好的感受到了异常值会如何影响我们的硬间隔SVM,那么我们现在就要考虑该如何解决异常值,或者是有重合的点对硬间隔SVM的影响。当我们重新考虑上图中我们的决定边界该如何定义时,我们发现最优的决定边界理应还是忽略唯一的异常值的硬间隔SVM的决策边界。于是,我们可以设计一种方法,使其允许一些点被错误的标记,并在损失函数中对其进行惩罚,以至于达到一个相对的平衡。假设我们对标记错误的点进行 C 倍的惩罚,当C 变小时,我们的算法会相对更少地惩罚错误标记的点,意味着可能会有更多的点被错误的标记;当C 变大时,我们的算法会更多地惩罚错误标记的点,意味着可能会有更少的点被错误标记;当 C 足够大之后,我们的算法得到的决定边界会和硬间隔SVM得到的决定边界一样。我们将这种允许错误标记点的算法称为软间隔支持向量机(Soft Margain SVM)。
在数学上,我们可以将以上的思想转化成为以下的最优化问题:
注:在我们的优化问题中,我们的有两个约束,分别是 和 。 如果我们忽略了其中任何一个约束的话,我们都将无法得到正确的解。
关于软间隔向量机损失函数的讨论
我们注意到在上面相较于硬间隔向量机,软间隔向量机增加了一项, 其中我们对于 的定义如下:
我们注意到,凡是被正确分类的点,我们都会有:
于是乎,我们就得到了一个关于 的特别的损失方程,这个损失方程的特点在于它只会惩罚被错误分类了的点,并且它的图像看起来很像一个铰链(hinge),于是乎我们称之为"hinge loss".
软向量机原问题(Primal Problem)的代码实现
xxxxxxxxxxD = X.shape[1]N = X.shape[0]W = cp.Variable(D)b = cp.Variable()# 在这里我们使用 C = 1/4C = 1/4loss = (0.5 * cp.sum_squares(W) + C * cp.sum(cp.pos(1 - cp.multiply(y, X * W + b))))# 在这里我们改变了损失函数,并且移除了对w和b的约束prob = cp.Problem(cp.Minimize(loss))prob.solve()# 转换w和b的值w = W.valueb = b.value# 画出决定边界x = np.linspace(-4, 4, 20)plt.plot(x, (-b - ((w[0]) * x)) / w[1], 'r', label="decision boundary for Soft Margain SVM")plt.legend()plt.show()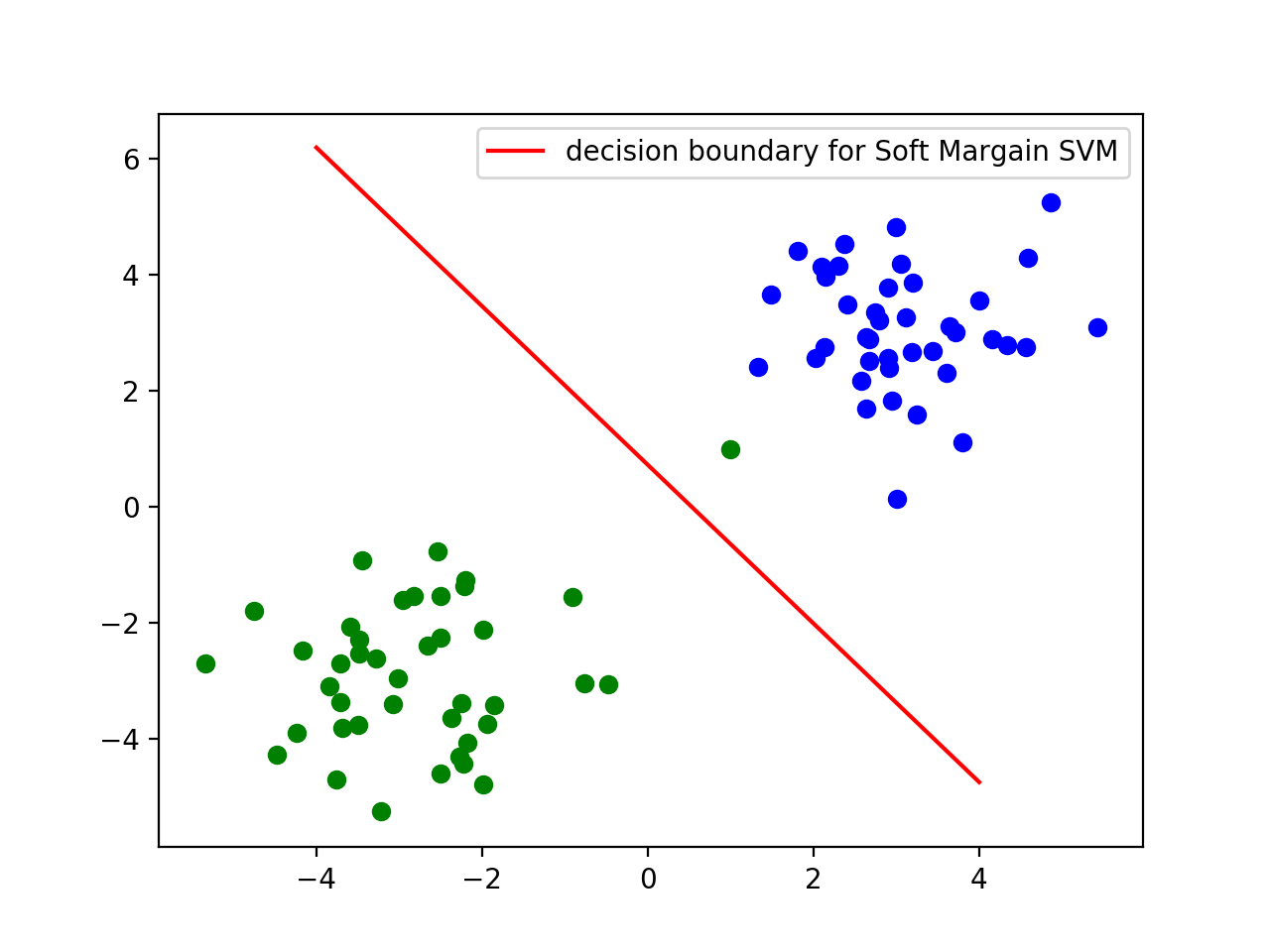
在上面的图中,我们可以看到我们的决定边界相比与有异常值的硬间隔SVM有了大幅度的提升,并且和最初没有异常值的硬间隔SVM的决定边界很接近,由此可见软间隔向量机可以大幅降低异常值对模型的损害。
在求解优化问题中,除了原问题的解法,我们是否还有别的解法呢?软间隔向量机对偶问题(Dual Problem).
现在我们重新回到我们的优化问题中:
我们发现我们的这个优化问题本质上其实是在求给定约束,然后求 的最小值。这个问题在数学上也是一个很重要的问题,并且法国数学家拉格朗日给出了拉格朗日乘数法(Larange Multiplier)的求解方法。在这里,我们一样可以应用该方法对本问题进行求解,我们称在求解最优化问题时应用拉格朗日乘数法的向量机问题为对偶问题(Dual Problem).
拉格朗日乘数法(Larange Multiplier)
我们回忆一下在高数中学到的拉格朗日乘数法:
我们会用到一个拉格朗日方程:
通过对方程两边求偏导,并且解方程组,我们就可以获得使得 最大的 x, y的最优解。
拉格朗日乘数法在对偶问题的应用:
让我们回到我们的最优解问题,我们可以得到如下的拉格朗日方程:
在求解拉格朗日方程时,我们需要其偏导等于0,即满足KKT条件:
经过化简,我们可以得到三个重要的结论:
然后我们将得到的三个结论带回我们的拉格朗日方程,并化简:
我们注意到我们的拉格朗日方程对 来说是线性的,所以我们无法将对 的偏导设为0。于是乎,我们就有了以下的一个新的最优解问题:
到这里,我们已经把对偶问题又成功转化成为了一个纯数学的最优化问题。
使用CVXOPT的软间隔向量机的对偶问题的实现.
在CVXOPT包中,有一个叫做"cvxopt_solvers.qp"的方程可以用来解以下问题:
我们发现这个方程所求解的函数和约束和我们最终转化的拉格朗日方程非常相似,我们可以通过改写我们的拉格朗日方程来符合本方程的输入,从而解得 的最大值。改写过程如下:
xxxxxxxxxximport cvxoptfrom cvxopt import matrix as cvxopt_matrixfrom cvxopt import solvers as cvxopt_solversdef LinearSVM_Dual(X, y, C): n, p = X.shape y = y.reshape(-1, 1) * 1. X_dash = y * X P = cvxopt_matrix(X_dash.dot(X_dash.T)) q = cvxopt_matrix(-np.ones((n, 1))) G = cvxopt_matrix(np.vstack((-np.diag(np.ones(n)), np.identity(n)))) h = cvxopt_matrix(np.hstack((np.zeros(n), np.ones(n) * C))) A = cvxopt_matrix(y.reshape(1, -1)) b = cvxopt_matrix(np.zeros(1)) cvxopt_solvers.options['show_progress'] = False cvxopt_solvers.options['abstol'] = 1e-10 cvxopt_solvers.options['reltol'] = 1e-10 cvxopt_solvers.options['feastol'] = 1e-10 sol = cvxopt_solvers.qp(P, q, G, h, A, b) alphas = np.array(sol['x']) sol_time = time.time() - start_time w = ((y * alphas).T @ X).reshape(-1, 1) # 我们选择一个合适的S的阈值,来矩阵中对小于阈值的数进行清零 S = (alphas > 1e-4).flatten() # 计算b的值 b = y[S] - np.dot(X[S], w) b = b[0] # 画出决定边界 x = np.linspace(-1, 5, 20) plt.plot(x, (-b - (w[0] * x)) / w[1], 'm') plt.show() return w, b我们画出的图与解出的 的值应该与原问题 (Primal Problem) 中相同,因为他们求的最优值问题相同,只是解法不同,故在此我们就不再此演示结果了。
至此,我们已经对SVM的几个重要的问题(硬间隔,软间隔(L1正则)的原问题和对偶问题)进行了讨论和实现,接下来我们会讨论一种不是很常见的软间隔(L2正则)问题。该问题更多在学习SVM的时候出现,我们对此做一个简单的介绍和讨论。如果不是写作业遇到了这个问题不会写,可以直接跳过本段。
支持向量机的L2正则形式
我们再次回顾一下我们刚刚建立的软间隔支持向量机,我们发现我们最后一项对标记错误的点的惩罚为: , 我们发现这个与L1正则中的惩罚相似,因此我们也称其为SVM的软间隔的L1正则。我们可以联想到,我们为了避免线性回归的过拟合,我们有L1正则(Lasso回归 Lasso Regression)和L2正则(岭回归 Rigde Regression)两个武器。
首先我们先回顾一下L1和L2正则的定义:
我们看到L1和L2正则对错误标记的点有不同的惩罚方式,所以在拉格朗日乘数方程中,我们需要满足不一样的KKT条件,从而得到最后不一样的拉格朗日方程的表达式,而它并不能直接通过粗暴的对以前的拉格朗日方程 项加平方得到,需要重新推导。
*特别注意:我们发现在L2正则中,我们取消了对 的约束。这里很有可能是作业中对此问题进行考察的点。在此我提出我的想法。首先我们是可以取消这个 的约束的,因为假设我们遇到了一个解,其中 , 那么 也一定可行;并且这个解会使L2的目标方程更小,即,我们可以舍弃 这和约束。
现在我们开始计算我们的L2正则的软间隔SVM的拉格朗日方程:
我们同样需要使得我们的拉格朗日方程对各个变量的偏导为0,即,满足KKT条件:
于是乎我们可以得到以下的目标方程:
我们依旧需要使用CVXOPT来求解我们的拉格朗日方程的最优化问题。首先,我们对我现有的式子进行变换可得:
现在我们可以代码实现我们的L2正则软间隔:
xxxxxxxxxximport cvxoptfrom cvxopt import matrix as cvxopt_matrixfrom cvxopt import solvers as cvxopt_solversdef l2_norm_LinearSVM_Dual(X, y, C): zero_tol = 1e-4 n, p = X.shape y = y.reshape(-1, 1) * 1. X_dash = y * X extra_term = 1/C * np.identity(n) P = cvxopt_matrix(X_dash.dot(X_dash.T) + extra_term) q = cvxopt_matrix(-np.ones((n, 1))) G = cvxopt_matrix(np.vstack((-np.diag(np.ones(n))))) h = cvxopt_matrix(np.hstack((np.zeros(n)))) A = cvxopt_matrix(y.reshape(1, -1)) b = cvxopt_matrix(np.zeros(1)) cvxopt_solvers.options['show_progress'] = False cvxopt_solvers.options['abstol'] = 1e-10 cvxopt_solvers.options['reltol'] = 1e-10 cvxopt_solvers.options['feastol'] = 1e-10 sol = cvxopt_solvers.qp(P, q, G, h, A, b) alphas = np.array(sol['x']) w = ((y * alphas).T @ X).reshape(-1, 1) # Selecting the set of indices S corresponding to non zero parameters S = (alphas > zero_tol).flatten() # Computing b b = y[S] - np.dot(X[S], w) b = b[0] # Display results x = np.linspace(-1, 5, 20) plt.plot(x, (-b - (w[0] * x)) / w[1], 'm') plt.show() return w, b
我们解决了所有线性可分的问题,那如果数据线性不可分呢?支持向量机的核方法
在我们继续讨论更多的支持向量机的之前,我们回归初心,一起整理一下我们是如何一步一步走到这里的。首先我们是为了解决“在不同类别点中寻找一个最优的界限”而提出的支持向量机的解法。然后我们针对最最简单的数据结构——两类完全线性可分、毫无重合、没有异常值的数据进行分类时提出了“硬间隔支持向量机”。然后考虑到该解法的应用场景很有局限性:无法分离有重合的数据集,并且会极大地受到异常值的影响,于是乎我们提出了更优的“软间隔向量机”的解法。 其中软间隔支持向量机增加了一项对错误标记的点的惩罚,对于不同的惩罚方式,我们引出了两种细分算法:“L1正则软间隔支持向量机,和L2正则软间隔支持向量机“。接着,我们在针对求解软间隔向量机的”最优化问题“时,我们又提出了两种不同的思路:直接求解的”原问题“,和使用拉格朗日乘数法的”对偶问题“。
至此,我们已经对所有的线性可分的数据给出了解法。那么随着数据的复杂,我们将面对无法用线性可分的数据集,那这个时候我们所有讨论过的方法都无法适用于此类问题。那么有什么解决方法呢?这个时候就引入了一个新的解决线性不可分的解法:核方法(Kernel)。
在我们正式的提出核方法前,我们先不妨尝试从直觉出发尝试一起解决一下这个问题,来建立一个对本问题的感觉,并且可以更好地学习并理解核方法。

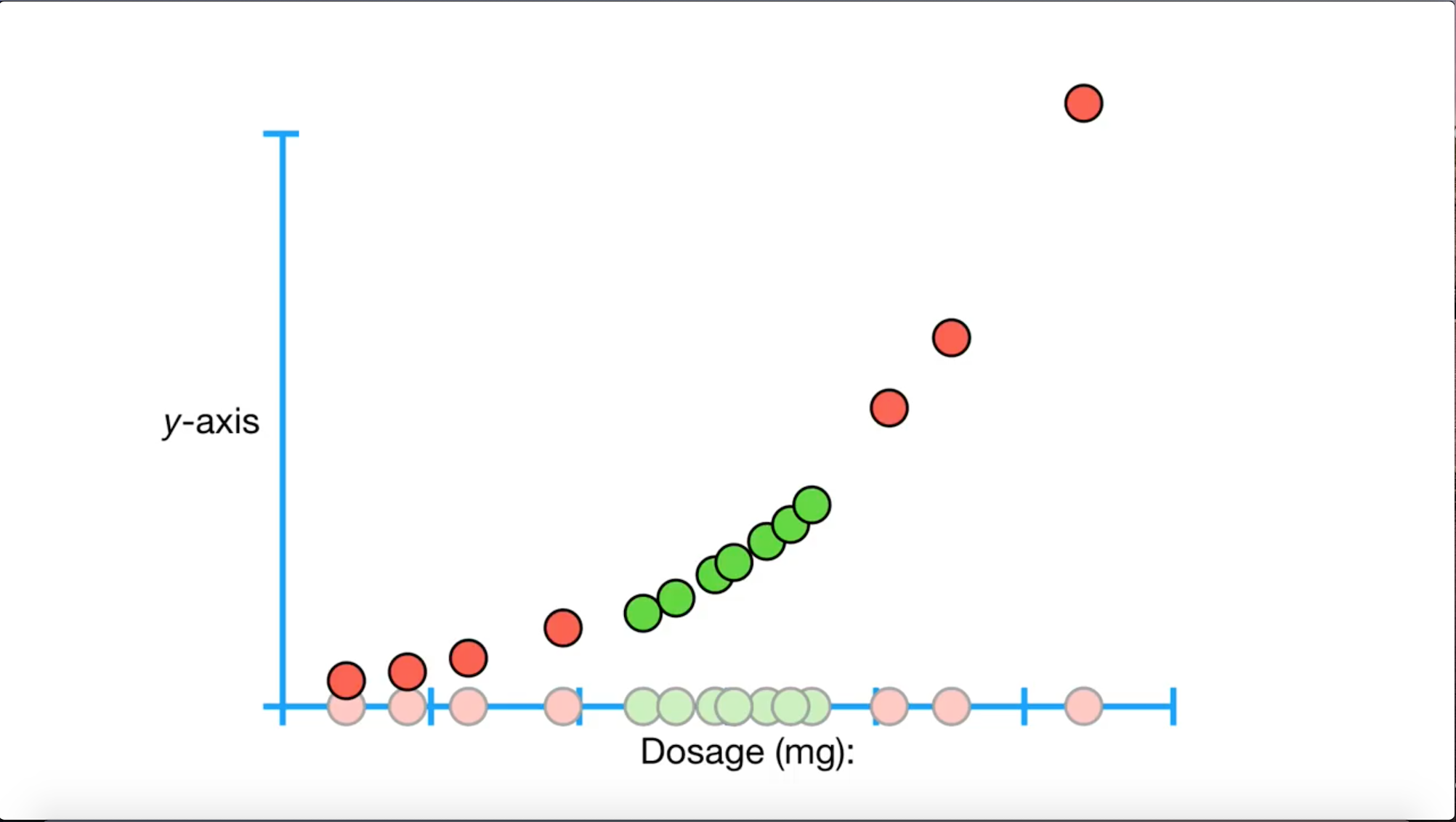
假设我们现在收集了一款药的用药剂量的数据,如上图,其中绿色的点代表合适的药量,红色的点表示不合适的药量。那么我们现在的问题就是寻找一个合适的边界,让我们可以知道合适的药量是多少?
经过前面我们的讨论,我们直觉上可能会想把红色点分为两组,一组在绿色的点左边,一组在绿色的点右边。这样我们就把这个线性不可分的问题转化成了两个线性可分的问题。也就是说,我们对第一组红点和全部绿点进行一次软间隔支持向量机,得到一个药量的下限的边界;再对第二组红点和全部绿点进行一次软间隔支持向量机,得到一个药量上线的边界;最后组合两次得到的边界,就可以得出最后合适药量的范围。
直觉上,我们目前感觉这个方法仿佛天衣无缝,但是当我们尝试考虑更高维的问题时——”在下图中在二维空间内分离红绿两点“时,我们就发现这个思路受到了极大地阻碍。按照这个思路来考虑,我们就需要找到无限多的过原点的线来帮助我们线性区分所有的点,比如:x轴,y轴,y=x, y=x... 然后我们需要把所有的点先映射到每一条线上,然后再进行数次软间隔支持向量机来得到在该直线上的分离,最后再组合所有得到的分割线,在2维空间中得到最终的答案。这显然无法实现,就算找到了实现方法,这个思路的运算时间会随着维度的增加而几何倍增长,故这个思路并不可行。
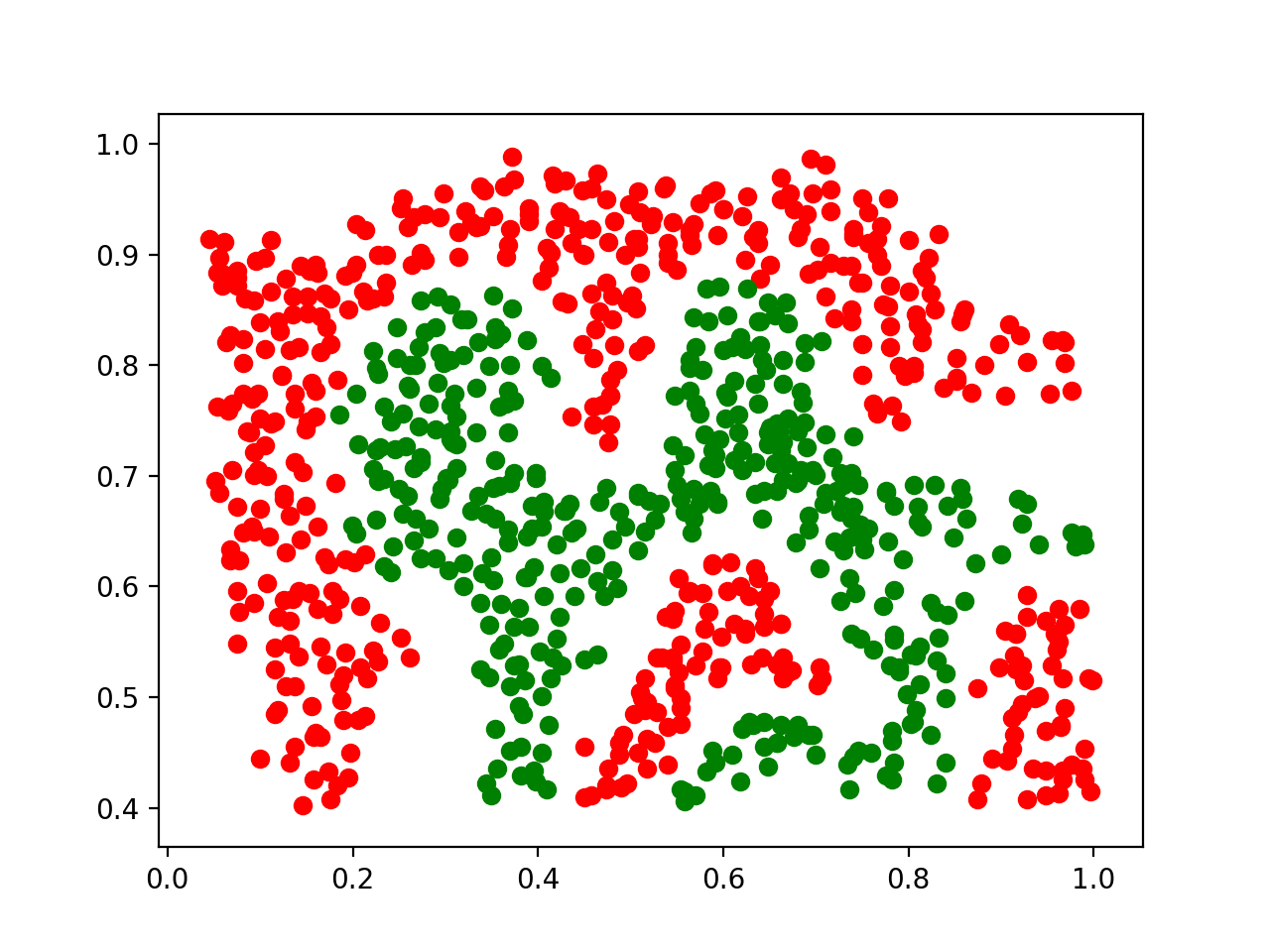
然而当我们反着思考刚刚的思路,假如我们不把”我们高纬度的点通过投射逐渐降为到1维,然后进行区分“,而是反着“把高纬的点投射到更高维的空间中,再更高维度空间中寻找线性可分的可能”呢?我们是否会有机会将本不能线性可分的数据在更高维变得线性可分呢?答案是肯定的。这就是核方法的核心思想。
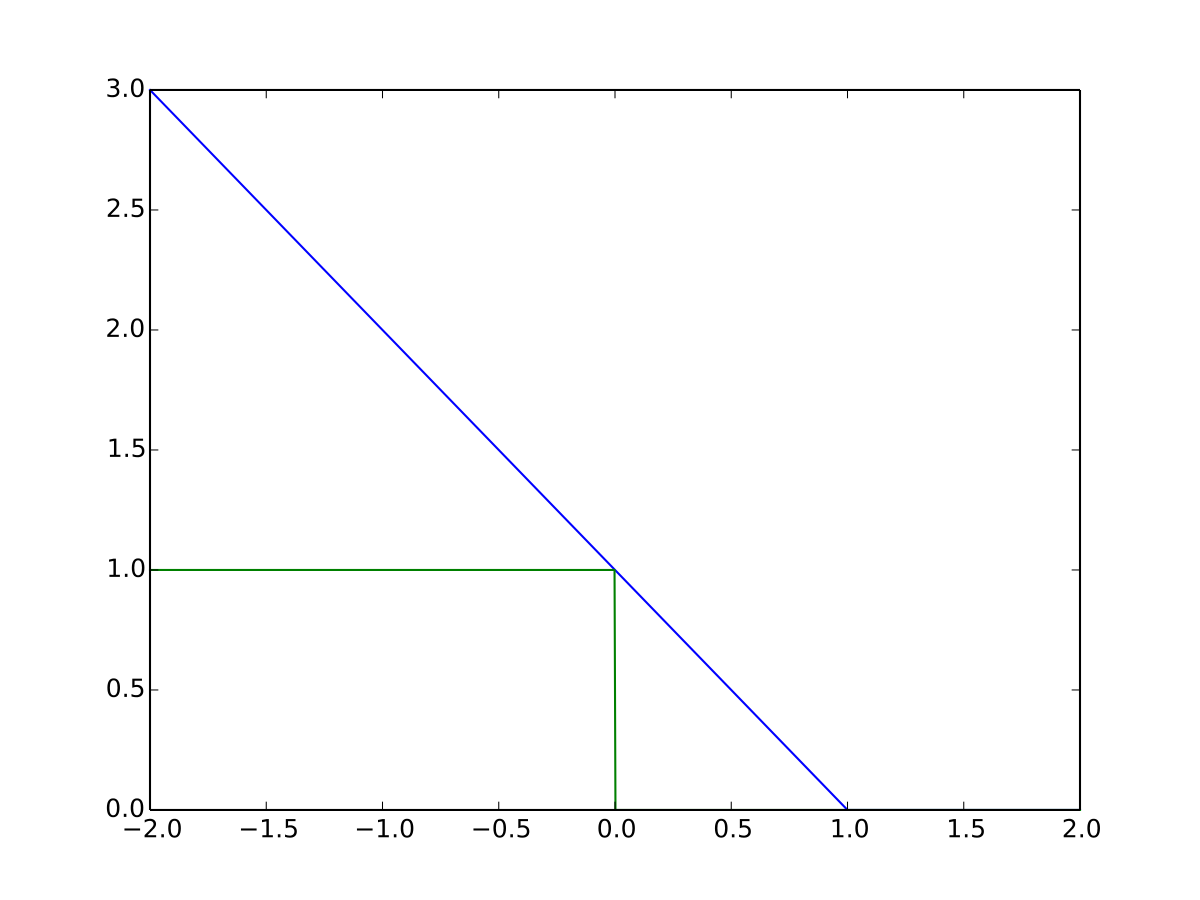
这虽然有些令人难以想象,但是我们不妨回到我们刚刚所用到的最简单的1维寻找药量的问题上。现在假设我们有一个方程 , 把所有在这条轴上的点映射到一条新的坐标y轴上(如下图),我们惊奇的发现我们的竟然可以用一条直线把我们投射的点分开,也就是我们将这个问题重新转换成为了我们已会的问题。
接下来,我们会问自己,那我们如何能找到合适的 去映射我们点呢?亦或是我们怎么知道,会是最合适的映射方程,为什么这个映射的方程不可以是 ?又或者是 呢 ?
寻找最佳的 的问题的答案在于使用高斯核。
核方法与对偶问题
我们在L1正则软间隔支持向量机中探讨了以下的最优解问题:
在核方法中,我们将优化的问题转化成为了以下问题:
我们注意到在核方法中,我们将原本的 替换成了 ,其中在这里作为我们的映射方程。的向量积则称为我们的核方程(Kernel function) .
核方法中不同的核方程
在经过一些对核方法有一些了解后,我们现在的目标转为了对核方程(Kernel function)的选择上。那么在这里,我们将介绍一些常见的核方程。
其中有多项核 polynomial kernel, . 同时还有关于 的Radial basis function kernel:。其中最重要的,我们还有高斯核 Gaussian Kernel,同时也叫“RBF”, 他的定义是:。
为什么高斯核区分线性不可分的数据时最好用?高斯核背后美丽的数学原理与代码实现
在此,我们将着重讨论一下在区分线性不可分的数据时表现最好的高斯核。我们对高斯核的讨论将分为三个部分。第一部分:我们将着重讨论高斯核背后美丽的数学原理;第二部分:我们将讨论如何代码实现高斯核;第三部分:我们将着重讨论如何在我们的支持向量机中使用高斯核,并且画出我们的非线性决策边界。
***注:如果你不是对这个算法的名称或者原理极为好奇,亦或是机器学习的课程中学到这个算法,需要对它有一个比较深的理解,那么你可以直接跳过前两部分,前两部分旨在解析高斯核的数学原理,与实际应用并无关联。
第一部分.为什么高斯核在区分线性不可分的数据时最好用?
首先我们对最基础的Polynomial Kernel 的一些性质进行讨论。
假定我们现在从基础的Polynomial Kernel出发:令 , 那么我们将会得到核方程 。我们可以发现这个其实是一个一维到一维的映射,把点的坐标映射到自己。或者说:假定有一点X在数轴上的坐标为2,那么经过映射后他的坐标还是2。
那么我们现在令 , 那么我们将会得到核方程 . 我们发现这个其实依旧是一个一维到一维的映射,他把每个点映射到坐标平方的点。或者说:假定有一点X在数轴上的坐标为2,那么经过映射后他的坐标将会变到4。

上图展示了在一维空间上两个点关于 的映射。我们可以发现,经过了的映射后,点与点之间的距离得到了增加,也就意味着经过一次平方的变换,曾经很密的点可能会变得稀松,换言之,变换过后的点可能会更便于分离。
我们发现无论我们怎么调整d的值,我们的映射依旧是从一维到一维的,即:。当我们尝试把两个核方程加到一起的时候,例如: 时,我们发现这个核方程是可以写成点乘: ,这就升级成为了一个从一维到二维的映射,即 。在这个映射之后的X坐标还是我们 的映射,而新增的Y坐标则是 的映射。
我们在前面发现了我们可以通过更高次项的Polynomial Kernel增加我们数据点和点之间的距离。同时假如我们的把我们的数据映射到更高维的空间,我们就可能可以在更高的维的空间对映射点做线性的分离。那如果我们把我们的数据映射到一个无限高维的 n维空间呢?我们也许可以寻找一个维的超平面对映射的点进行线性分离。换言之,任何维度无法线性可分的数据,在映射到一个无限高维的n维空间之后也许都可以找到一个(n-1)维的超平面进行线性分离,从而解决非线性可分的问题。
那么我们假设我们现在的核方程是由 不同的Polynomial Kernel相加而成,即:
我们尝试一下从另一个角度出发,首先我们先回忆一下 的泰勒展开:
当我们在 的时候进行泰勒展开,我们有:
我们发现这个泰勒展开可以重写成:
假如我们定义一个常数项 , 并把它带入上面的泰勒展开中,我们可以获得:
我们很惊奇的发现,我们的高斯核竟然可以展开成为一个到无穷高的 n维空间 () 的映射, 也就说我们就可以通过高斯核进行我们理想中的在无穷高维空间寻找映射后的点线性可分的超平面了。
不得不感叹,虽然很多数学学不会,但是他是真的很美丽!
第二部分:代码实现高斯核
手动实现高斯核,我们有:
xxxxxxxxxxdef gaussianKernel(X1, X2, sigma=0.1): gram_matrix = np.zeros((X1.shape[0], X2.shape[0])) for i, x1 in enumerate(X1): for j, x2 in enumerate(X2): x1 = x1.flatten() x2 = x2.flatten() gram_matrix[i, j] = np.exp(- np.sum(np.power((x1 - x2), 2)) / float(2*(sigma**2))) return gram_matrix
第三部分:高斯核在支持向量机中的应用。
x
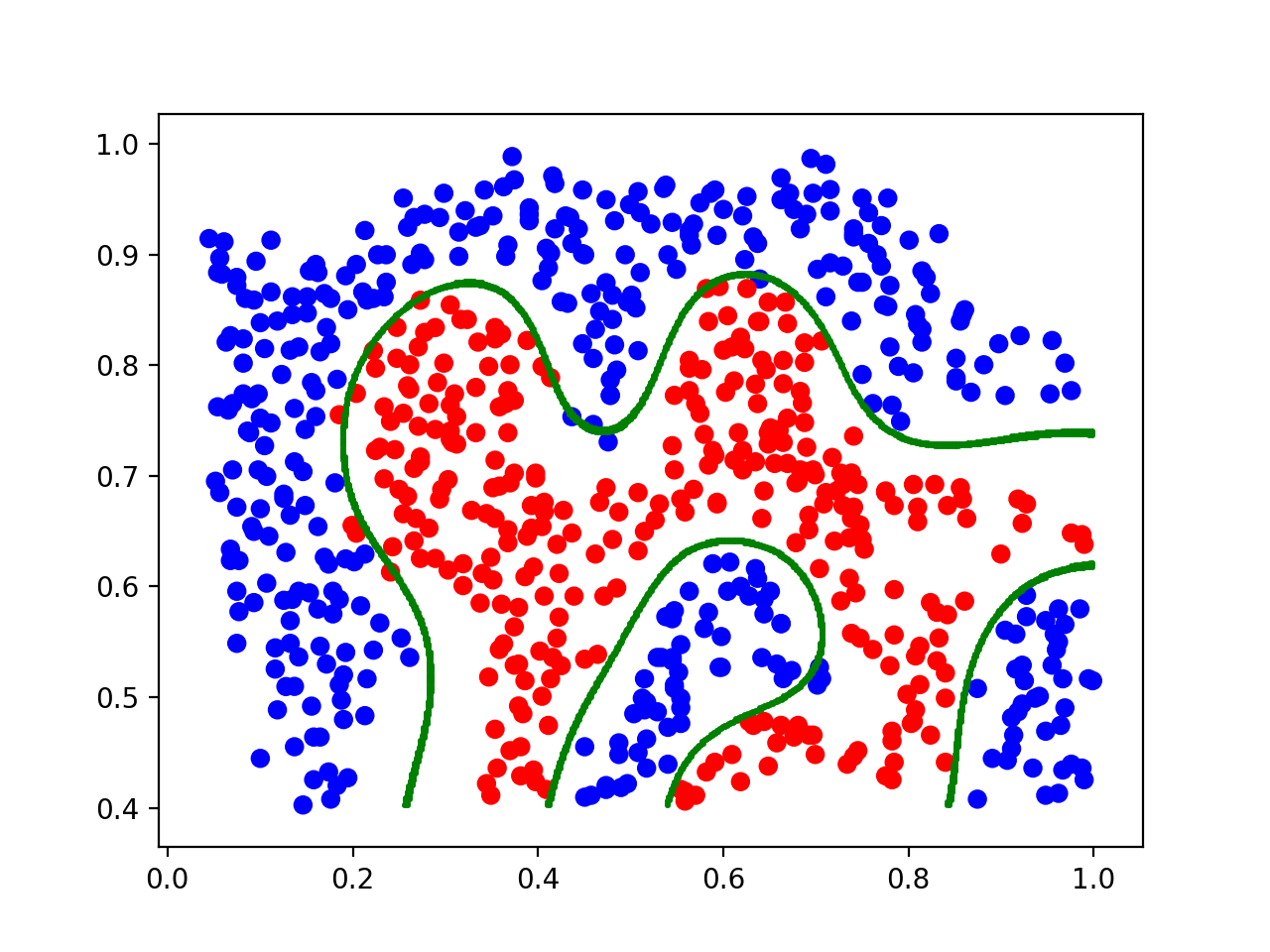
import pandas as pddata2 = pd.read_csv('prob2data.csv', header=None).valuesX = data2[:, 0:2]y = data2[:, -1]# 首先把数据变成符合要求的for i in range(len(y)): if y[i] != 1: y[i] = -1def customized_kernel_svm(): # 在这里我们使用 “rbf” 核作为我们的高斯核 # 我们在这里使用的是gamma,而不是在实现高斯核中的 sigma。 其中我们可以通过 gamma = 1/2 sigma 来计算和转化sigma到gamma。 clf = SVC(kernel="rbf", gamma=20, C=1) X, y = X_train, y_train clf.fit(X, y) x1s = np.linspace(min(X[:, 0]), max(X[:, 0]), 600) x2s = np.linspace(min(X[:, 1]), max(X[:, 1]), 600) points = np.array([[x1, x2] for x1 in x1s for x2 in x2s]) # 计算决策边界 dist_bias = clf.decision_function(points) bounds_bias = np.array([pt for pt, dist in zip(points, dist_bias) if abs(dist) < 0.05]) # 画出决策边界 plt.scatter(X[:, 0], X[:, 1], color=["r" if y_point == -1 else "b" for y_point in y], label="data") plt.scatter(bounds_bias[:, 0], bounds_bias[:, 1], color="g", s=0.5, label="decision boundary") plt.show()
作为结果,你应该可以预计如下的图像。
结语
好的,当你看到这里的时候,恭喜你已经对“在数据中寻找合适的界限”这个问题,亦或是“支持向量机”有了一个很深入的理解了!恭喜!
希望你可以开始上手做一做属于自己模型,并希望你在未来可以得心应手的解决此类问题。
加油!